遠程醫療的復雜環境中，心電信號極易被噪聲淹沒，從而影響心血管疾病的智能診斷。基于此，本文提出了一種基于遞歸最小二乘法的回聲狀態網絡心電信號降噪算法。該算法通過遞歸最小二乘法對該網絡進行訓練，可自動學習得到含噪心電數據中非線性的且具有區分度的深層次特征，并利用這些特征自動分離心電信號與噪聲。實驗中，采用信噪比和均方根誤差為指標，將本文方法與基于子帶自適應閾值的小波變換法和 S 變換法進行比較。實驗結果表明，本方法降噪精度更優，同時信號的低頻成分也得到了很好的保持。本文方法可做到消除心電信號中的復雜噪聲并完整保留心電信號的形態，為心電圖的特征檢測和心血管疾病的智能診斷奠定了基礎。
引用本文： 張杰爍, 劉明, 李鑫, 熊鵬, 劉秀玲. 基于遞歸最小二乘法的回聲狀態網絡算法用于心電信號降噪. 生物醫學工程學雜志, 2018, 35(4): 539-549. doi: 10.7507/1001-5515.201710072 復制
引言
目前，由心血管病引起的死亡已占城鄉居民死亡構成的首位，并且心血管病患病率及死亡率仍處于上升階段[1]。動態心電圖（electrocardiogram，ECG）作為應用范圍最廣的診斷心血管疾病的重要無創性手段，其信號的低頻成分的變化對心血管疾病的智能診斷至關重要，例如 ST 段的變化是利用動態 ECG 信號診斷心肌梗死的重要指標之一[2]。如今，遠程醫療的發展為動態 ECG 信號的長期監測提供了平臺。但與此同時，遠程醫療背景下的信號采集和傳輸也混雜了多種因素造成的復雜噪聲，并且這些復雜噪聲也極易淹沒 ECG 信號的主要特征，特別是例如 P波、T 波等低頻成分。因此，如何消除 ECG 信號中的復雜噪聲，并完整保留 ECG 信號的主要特征，成為當前醫學信息處理領域亟待解決的難題。
目前，用于 ECG 信號降噪的方法主要有：人工神經網絡（artificial neural networks，ANN）、集合經驗模式分解（ensemble empirical mode decomposition，EEMD）、主成分分析（principal component analysis，PCA）、獨立成分分析（independent component analysis，ICA）、傅里葉變換、S 變換和小波變換等[3-11]。Jebaraj 等[4]利用 EEMD 將含噪 ECG 信號分解為若干個不同時間尺度的固有模態函數（intrinsic mode function，IMF），然后將這些 IMF 中含有噪聲的舍棄，最終能夠濾除含噪信號中 60 Hz 的電力線干擾。但是，在舍棄的 IMF 中也會含有與低頻噪聲的頻率相似的 ECG 的 P 波和 T 波，這就導致重構的 ECG 信號不完整。而 PCA 和 ICA 都是用于從非高斯噪聲信號中尋找獨立的源信號的盲源分離技術，能夠濾除與 ECG 信號統計不相關的噪聲[5-6]。但是，該類方法的魯棒性低，對于含噪 ECG 信號的細微變化十分敏感，并不適用于遠程醫療背景下 ECG 信號中含有復雜噪聲的情況。Alyasseri 等[11]首先利用 β 爬山算法選擇的最優的小波基將含噪 ECG 信號由時域變換到頻域的不同尺度中，再利用閾值保留主要由有效信號控制的小波系數，最終該方法在去除高頻大噪聲方面取得了不錯的結果。但對于 ECG 信號和噪聲的頻帶相互重疊的情況，主要保留的小波系數仍然含有部分噪聲信息，這也就必然導致重構的 ECG 信號的低頻成分存在形態失真。基于以上分析，現有研究成果在降噪精度上均得到了較滿意的效果，但并沒有過多地關注于 ECG 信號的低頻成分保持問題。
因此，為了進一步提高在遠程醫療背景下被復雜噪聲污染的 ECG 信號的降噪效果，尤其是對 ECG 信號低頻成分的保持，本文提出了基于遞歸最小二乘（recursive least square，RLS）的回聲狀態網絡（echo state network，ESN）算法——RLS-ESN 算法。該方法利用 RLS 來訓練 ESN，從而使網絡自動學習采集到的含噪 ECG 數據中非線性的且具有區分度的深層次特征，最后網絡利用這些能夠區分 ECG 信號和噪聲的特征自動重構得到干凈的 ECG 信號。
1 方法
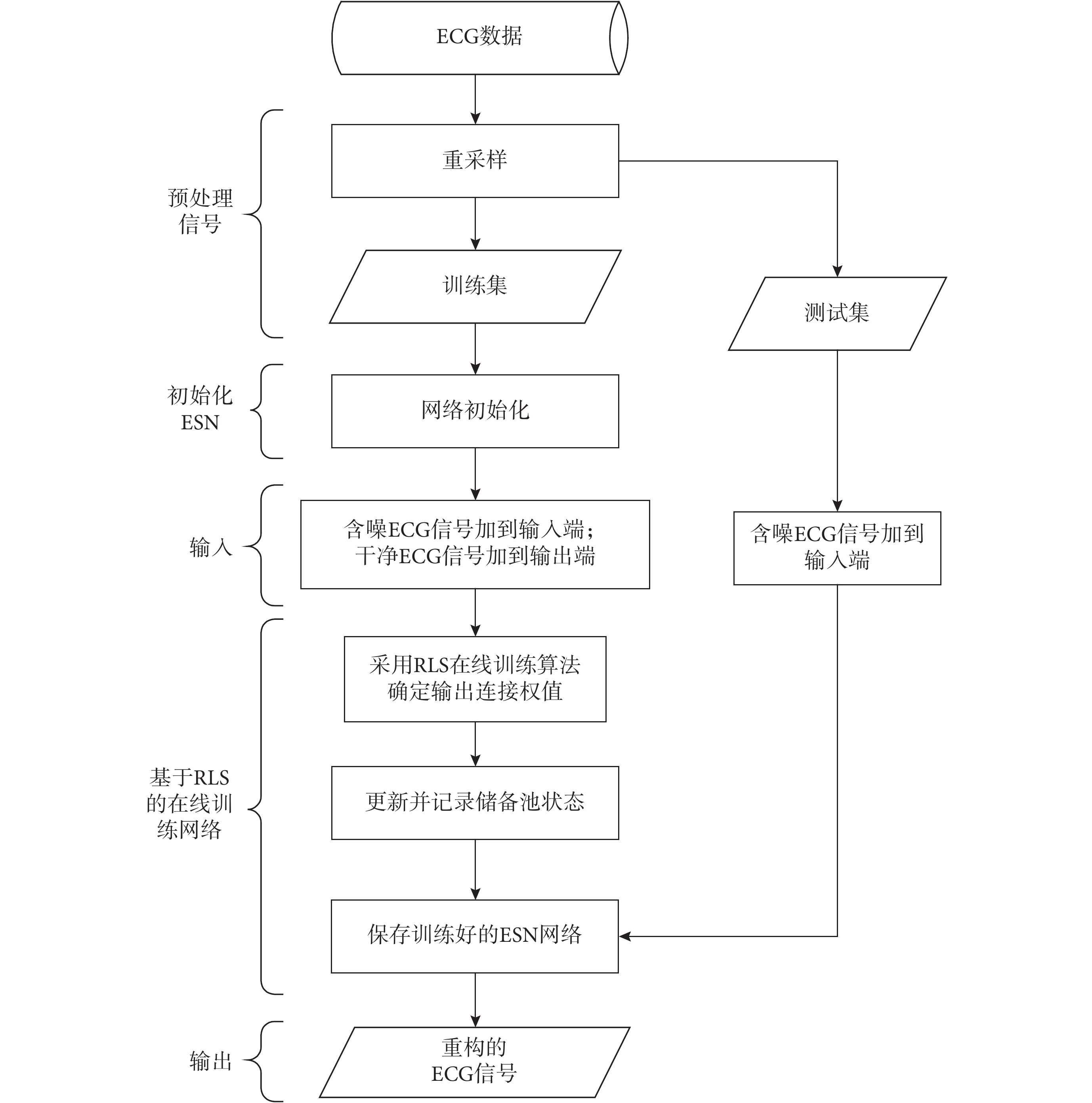
如圖 1 所示，基于 RLS 在線訓練算法的 ESN 降噪框圖主要由 4 部分組成：預處理信號、初始化 ESN、構建輸入輸出函數和基于 RLS 的在線訓練網絡。首先，由于過大的采樣頻率會造成 ECG 信號中冗余信息增多降低網絡運行效率，而過小的采樣頻率又會丟失 ECG 信號中有效信息，因此本文算法對 ECG 信號以合適的 250 Hz 的采樣頻率進行重采樣；其次，依據網絡參數的范圍設置合適的 ESN 網絡參數；然后，為了更符合現實需求和 ECG 信號非平穩信號的特點，采用了逐個處理信號的 RLS 在線訓練算法對 ESN 進行訓練，利用儲備池的稀疏性能得到含噪 ECG 數據中非線性的且具有區分度的深層次特征，并且通過訓練得到最優的輸出權值矩陣，保存訓練好的 ESN 網絡；最后，將測試集中含噪 ECG 信號輸入訓練好的 ESN 網絡，利用儲備池得到能夠區分 ECG 信號和噪聲的特征后，訓練好的 ESN 網絡再利用輸出權值矩陣重構得到干凈的 ECG 信號。
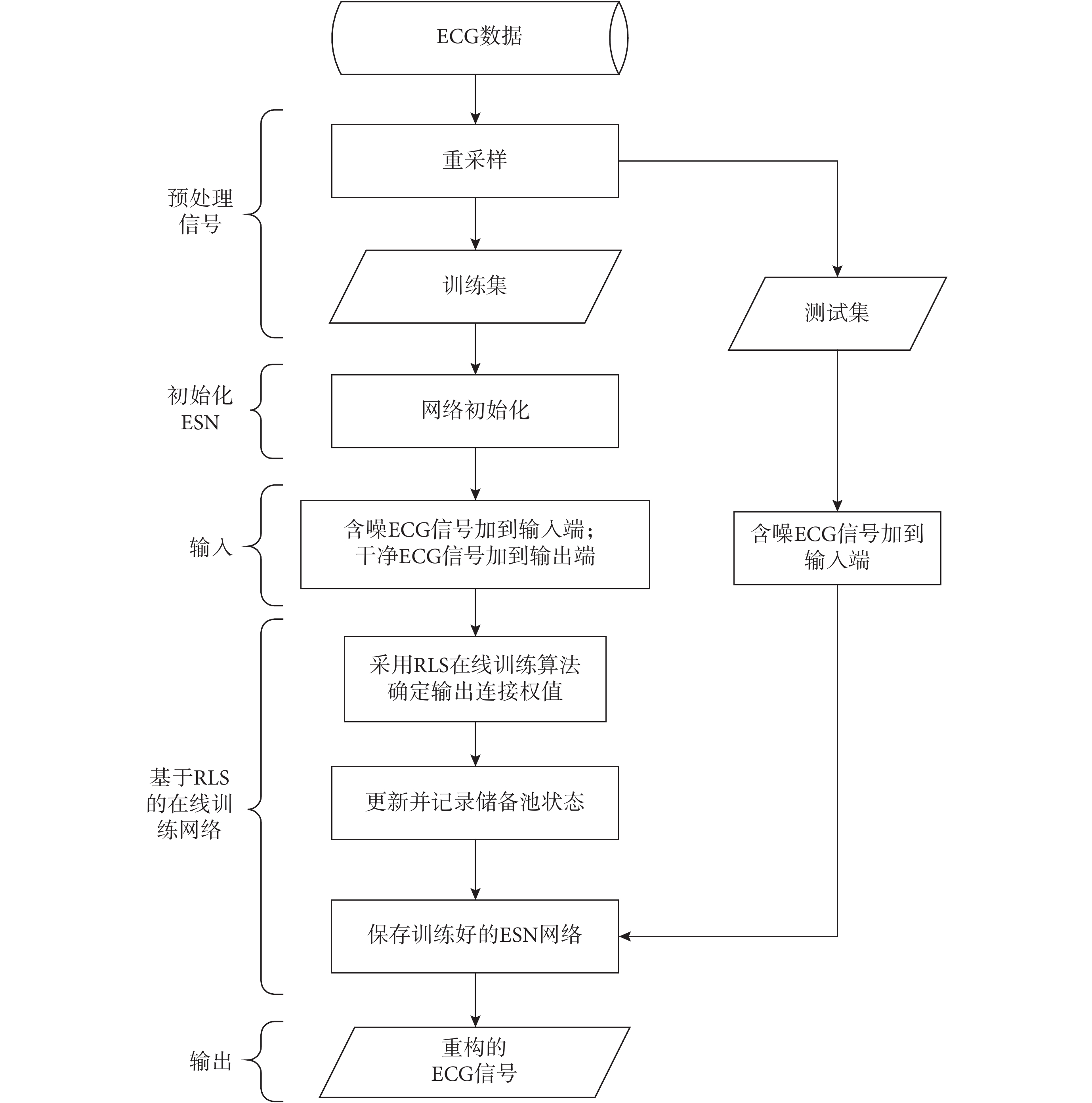圖1
基于 RLS 在線訓練算法的 ESN 降噪框圖
Figure1.
ECG signal filter block diagram of ESN with RLS online training algorithm
1.1 數據來源
本文實驗中使用的 ECG 信號來自美國麻省理工學院與貝斯以色列醫院（Massachusetts Institute of Technology and Beth Israel Hospital，MIT-BIH）聯合構建的數據庫中的心律失常數據庫（Arrhythmia Database）（網址為：https://www.physionet.org/physiobank/database/mitdb/），該數據庫中包括 48 組采樣頻率為 360 Hz 并且數據長度為 30 min 的動態 ECG 信號記錄，每組記錄包括來自醫用的 24 h 動態 ECG 信號記錄儀的 12 導聯數據中的兩個導聯信號：第一個導聯信號為修正的肢體Ⅱ導聯，第二個導聯信號為胸部 V2 導聯或胸部 V5 導聯[12]。為了與已有文獻中的采用基于子帶自適應閾值的小波變換（wavelet transform with subband dependent threshold，WT-Subband）降噪算法和 S 變換降噪算法進行比較，本文對應展示了 9 個 ECG 數據的實驗結果，分別為：103 號、105 號、111 號、116 號、122 號、205 號、213 號、219 號、223 號。
實驗中采用的噪聲信號來自于 MIT-BIH 數據庫中的噪聲壓力數據庫（Noise Stress Test Database）（網址為：https://www.physionet.org/physiobank/database/nstdb/），其中包括 3 h 的動態 ECG 信號記錄噪聲數據，分別為基線漂移（baseline wander，BW）、肌電干擾（muscle artifacts，MA）和電極干擾（electrode motion，EM）共 3 種噪聲數據。
1.2 基于 RLS-ESN 的 ECG 信號降噪算法
ESN 作為深度學習的主流模型之一，不但具有基于醫療大數據背景下數據增多效果更優的特點，而且還具有求解過程簡單且訓練速度快的特點。它的獨特之處在于其是采用由隨機稀疏連接的神經元組成的儲備池來代替傳統神經網絡中的隱藏層，并且唯一需要訓練的參數只有輸出權值矩陣，因此大大簡化了網絡權值的求解過程和訓練算法[13-14]。基于 ESN 的降噪算法是通過訓練網絡參數自動學習得到含噪 ECG 數據中非線性的且具有區分度的深層次特征，并利用這些特征以實現將 ECG 信號與噪聲分離的目的。
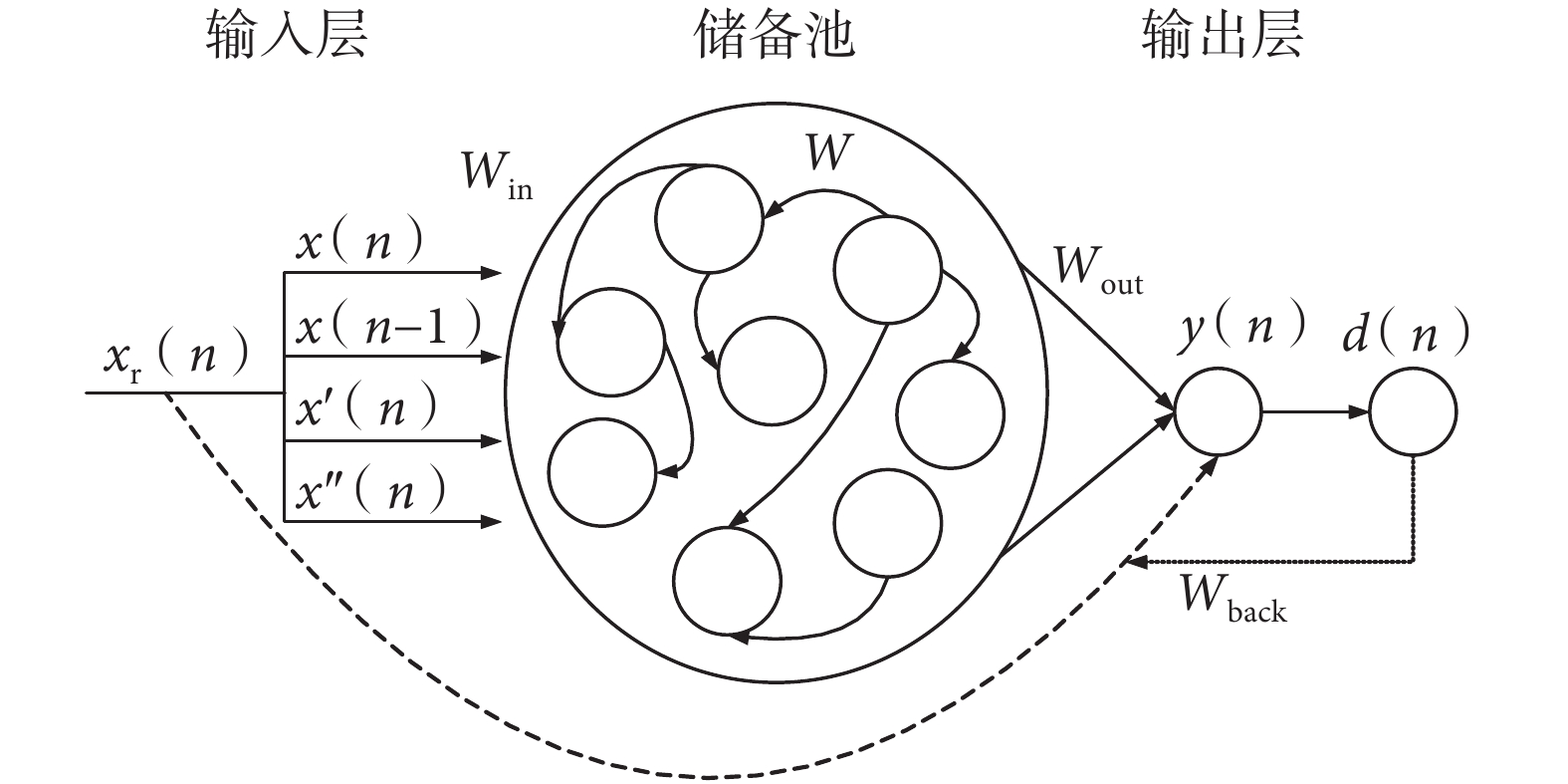
本文提出了基于 RLS 的在線訓練算法完成 ESN 降噪模型的權重更新。相比于離線訓練算法一次性的處理所有的輸入信號，以序列化的方式逐個處理輸入信號的基于 RLS 的在線算法更適合于目前信息處理的需求[15]。并且 RLS 的基本思想是在每個時刻對所有已輸入信號而言重估的平方誤差的加權和最小，這使得其對 ECG 信號這種非平穩信號的適應性非常好[16]。基于 RLS 在線訓練算法的 ESN 降噪模型的結構圖如圖 2 所示。
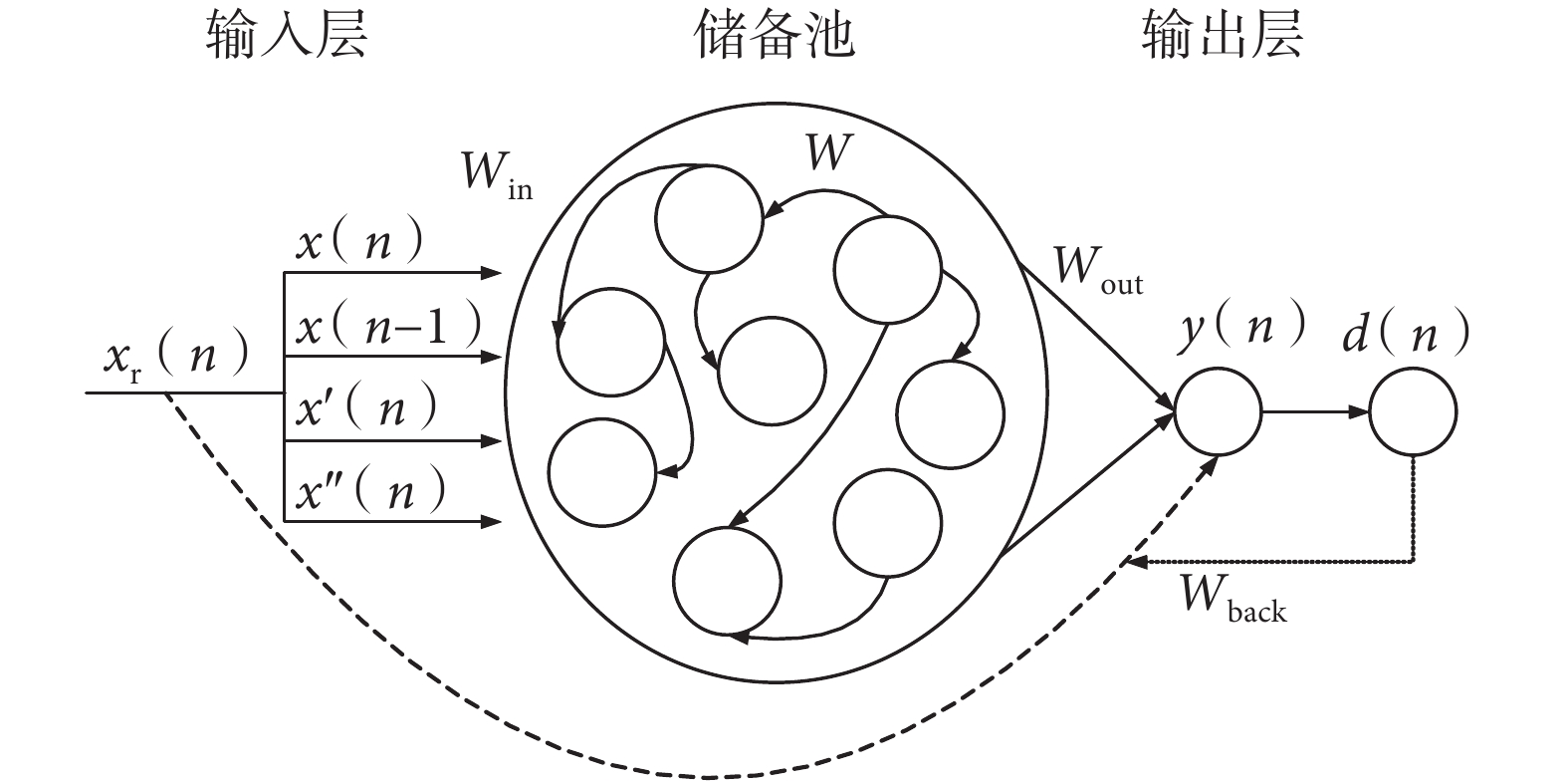圖2
基于 RLS 在線訓練算法的 ESN 結構圖
Figure2.
The structure of ESN based on RLS online training algorithm
1.2.1 信號預處理
作為一種準周期性信號，ECG 信號有效信息主要分布在 P-QRS-T 波群中，冗余信息主要體現在相鄰樣本點之間的相關性和相鄰心拍之間的相似性[17]。因此，在處理同等時間長度的 ECG 信號時，過大的采樣頻率會導致數據冗余增多，并且冗余信息的增多不僅沒有為 ESN 降噪模型增添新的特征，反而會增大儲備池維度，降低 ESN 的計算速率增大計算誤差導致網絡運行性能降低；而過小的采樣頻率則直接會導致 ECG 信號中相關性等特征信息的丟失。
基于此，Petr?nas 等[18]根據人的心理電活動周期并且經過多次試驗得出，當 ECG 信號的頻率為 250 Hz 時，可以在包含 ECG 信號主要特征的前提下使用較低緯度的儲備池，以保證 ESN 的高效運行。因此本文預處理時，首先將 MIT-BIH 庫中的 48 組 ECG 數據以及 3 種噪聲數據重采樣為 250 Hz。然后，將 3 種噪聲數據按照一定的信噪比（signal-to-noise ratio，SNR）（以符號 SNR 表示）疊加到心律失常數據庫中的 48 組 ECG 信號上，即可得到含噪 ECG 信號。最后，利用每個原始 ECG 數據的前 3 min 信號和相應的含噪 ECG 數據的前 3 min 信號組成訓練集，剩余的含噪 ECG 信號組成測試集。
1.2.2 ESN 降噪模型的初始化
為消除 ECG 信號中的噪聲，需構建基于 RLS 在線訓練算法的 ESN 降噪模型。首先，進行參數的初始化。ESN 的主要參數包括：儲備池規模、儲備池稀疏程度、儲備池譜半徑和儲備池輸入單元尺度[19]。儲備池規模（符號記為：N）定義為儲備池中的神經元的個數，在儲備池內部通過這 N 個神經元之間稀疏連接形成 N × N 的儲備池內部神經元連接權值矩陣 W。儲備池稀疏程度（符號記為：SD）定義為儲備池中相互連接的神經元個數與總神經元個數之比，表達式為 SD = m/N，通常 SD 的取值為 1%～5%。儲備池譜半徑（符號記為：SR）定義為 W 的最大特征值的絕對值，表達式為 SR = max{abs（W 的特征值）}，且當 SR < 1 時，ESN 才具有回聲狀態性質。儲備池輸入單元尺度（符號記為： IS）是一個尺度因子，在輸入信號連接至儲備池之前與輸入信號相乘，將輸入信號變換至神經元激活函數相應的范圍內。
其次，進行權值矩陣的初始化。輸入單元與儲備池內部連接的的權值矩陣 Win 和儲備池內部神經元連接權值矩陣 W 的初始化都是隨機且服從均勻分布的，且初始給定后固定不變。而儲備池與輸出單元連接權值矩陣 Wout 和輸出單元與儲備池的連接權值矩陣 Wback 初始化為零矩陣，其中 Wout 通過訓練得到其最終值。
1.2.3 輸入輸出信號的構建
ESN 的輸入信號 xr（n）的表達式如式（1）所示。其中，x（n）為當前時刻的含噪 ECG 信號；x（n-1）為上一時刻的含噪 ECG 信號；x′（n）和 x″（n）分別為 x（n）的一階導和二階導，表征了 x（n）的細節特征。
'/> |
輸出信號 y（n）為濾波后的 ECG 信號，定義如式（2）所示：
 |
其中， g（·）為激活函數，在實驗中選為恒等函數，即輸出神經元為一個線性神經元；矩陣 v（n）的表達式為
，其中 r（n）是儲備池的狀態矩陣。
誤差定義為當前時刻的干凈 ECG 信號 d（n）與 y（n）的差值，表達式為 e（n）= d（n）– y（n），其中 d（n）為當前時刻的干凈 ECG 信號。因此，在訓練中需要通過更新 Wout 和 r（n）使濾波后的 ECG 信號 y（n）逼近干凈 ECG 信號 d（n），使誤差 e（n）能夠近似于 0。
1.2.4 基于 RLS 的在線訓練
在本文中，輸出權重 Wout 的更新選用基于 RLS 的在線訓練算法[20]。具體過程如下：
（1）u（n）的表達式為
，其中 ψ（n）為 v（n）的相關系數矩陣的逆矩陣，并且 ψ（n）的更新如式（3）、式（4）所示：
 |
 |
式中的遺忘因子
定義為一個范圍為 0.95 <
< 1 的常數。設定
，其中 I 為單位矩陣，δ 為一個極小的正數。
（2）輸出權重的更新如式（5）所示：
 |
（3）儲備池狀態矩陣 r（n）的更新，如式（6）所示：
 |
其中 Win 為 4 × N 的輸入權值矩陣；W 為 N × N 的儲備池內部權值矩陣；f（·）為儲備池的激活函數，在實驗中選為非線性的 tanh（·）函數；遺忘率
被定義為一個小于 1 的正數。
2 結果與討論
2.1 性能指標
通過比較濾波后的信號與原始信號之間的 SNR 和均方根誤差（root mean square error，RMSE）（以符號 RMSE 表示）來評估本文降噪算法的性能。若 di 表示干凈 ECG 信號，yi 表示經過網絡降噪后的估計 ECG 信號，SNR 定義為信號和噪聲的比值，單位為分貝（dB），作為評價信號質量的重要指標，SNR 值越高說明濾波效果越好，表達式如式（7）所示：
 |
RMSE 是一個無量綱參數，定義為估計信號和真實信號的差值，越低則說明濾波性能越好，表達式如式（8）所示：
 |
2.2 實驗結果與討論
本文經過多次實驗后，網絡參數初始化為 SR = 0.4，SD = 2%，λ = 0.999 9，δ = 0.001 72，α = 0.8，IS = ［0.01；0.01；0.9；0.8］，輸入神經元個數為 4，儲備池規模 N 為 1 000，輸出神經元個數為 1。
2.2.1 實驗結果
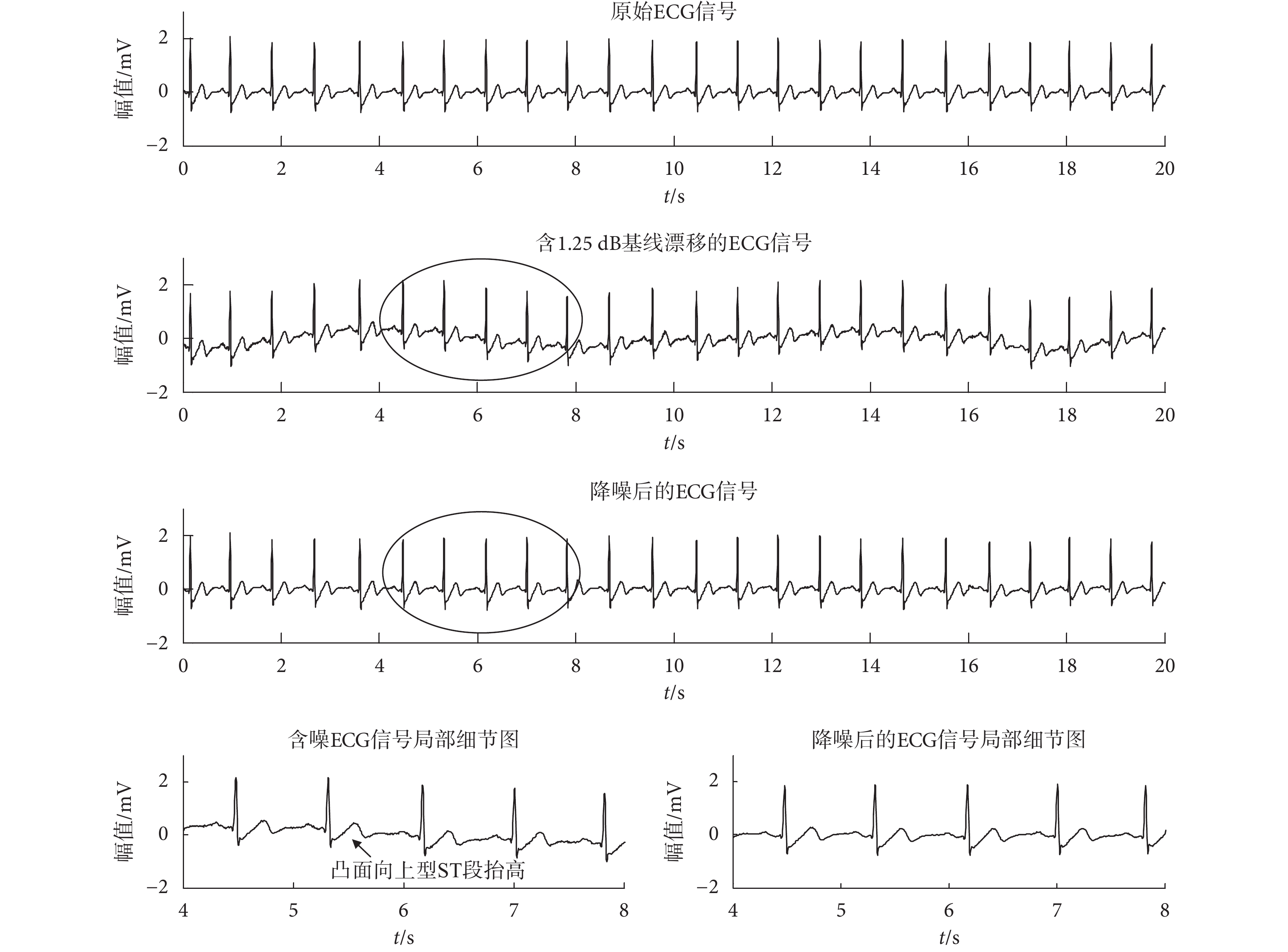
濾除 1.25 dB 基線漂移的實驗結果如圖 3 所示。其中，含噪 ECG 信號和原始 ECG 信號（以 MIT-BIH 數據庫中 103 號為例）相比較可以看出，基線漂移的存在已經影響了整體波形的走勢；并且由含噪信號的局部細節圖可以看出，基線漂移使得正常的 ST 段抬高成為凸面向上型。但經過本文提出的基于 RLS 在線訓練算法的 ESN 降噪算法降噪后的 ECG 信號和原始 ECG 信號相比較可以看出，降噪后的信號回到了基線，且形態和原始信號基本保持一致，尤其從降噪后的 ECG 信號的局部細節圖可以發現，ECG 信號的 ST 段已恢復為正常的波形。
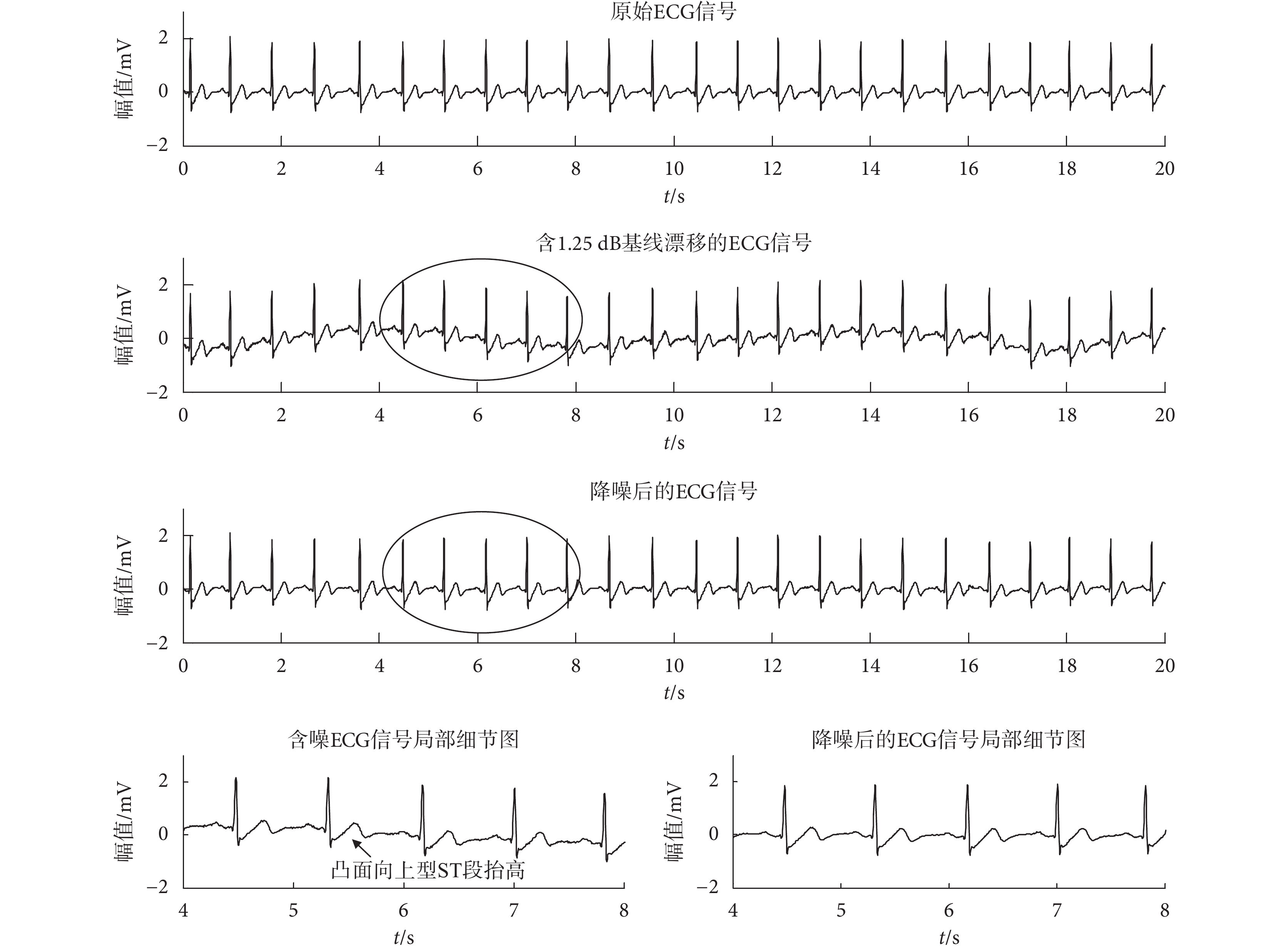圖3
濾除基線漂移結果圖
Figure3.
Experimental results for baseline wander noise case
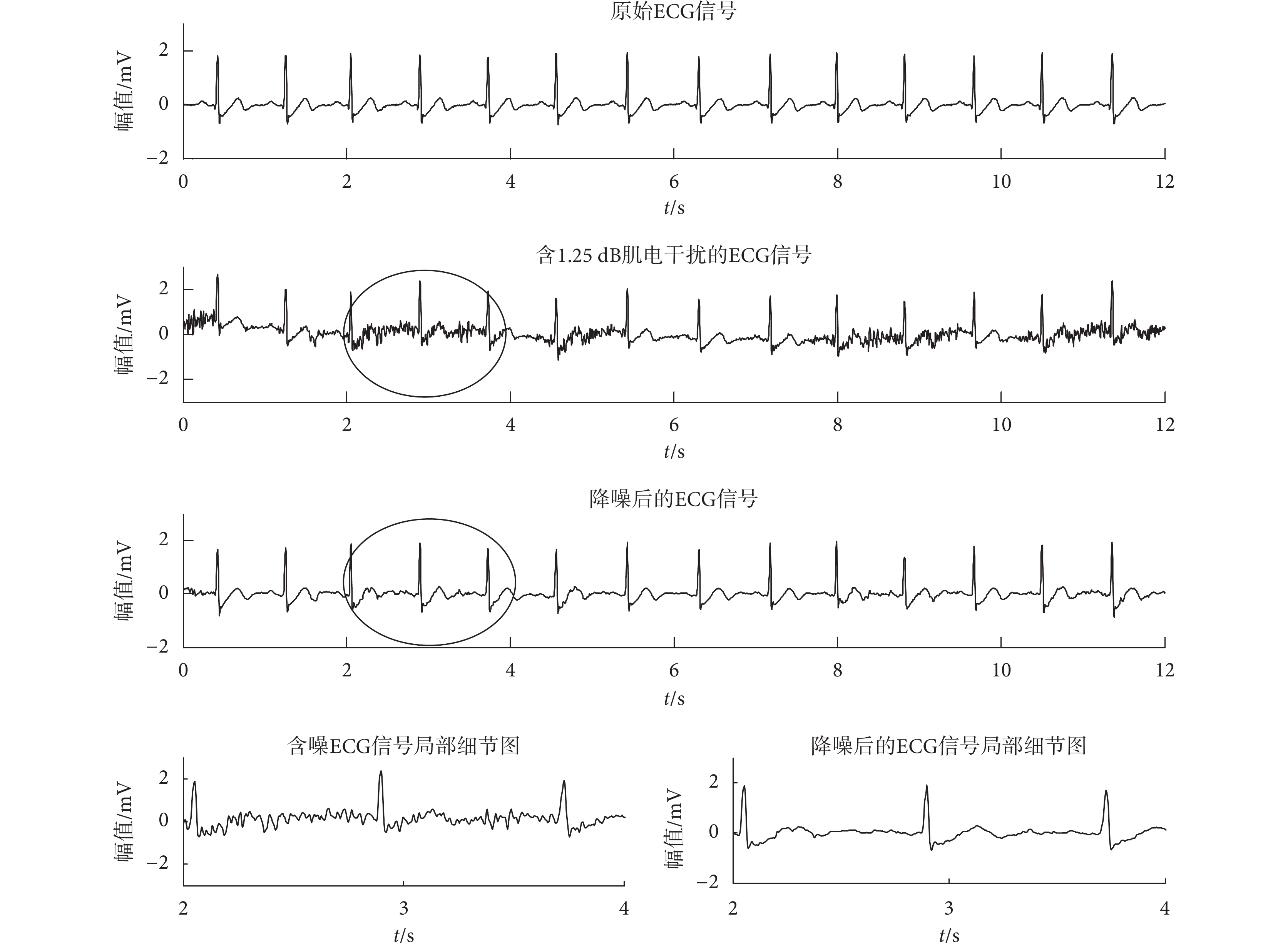
濾除 1.25 dB 肌電干擾的實驗結果如圖 4 所示。其中，含噪 ECG 信號和原始 ECG 信號（以 103 號為例）相比較可以看出，肌電干擾已嚴重破壞了 ECG 信號中特征波的形態；并且由含噪 ECG 信號的局部細節圖可以發現，Q 波和 S 波、P 波、T 波等低頻成分已經被肌電干擾完全淹沒，僅剩下了幅值較大的 R 波，造成了 ECG 信號的低頻特征丟失。但經過本文提出的基于 RLS 在線訓練算法的 ESN 降噪算法降噪后的 ECG 信號和原始 ECG 信號相比較可以看出，本文的降噪算法在濾除肌電干擾時，完整地保留了原有波形的形態特征，尤其從降噪后的 ECG 信號的局部細節圖可以發現，ECG 信號的低頻波形特征也得到了很好的保留。
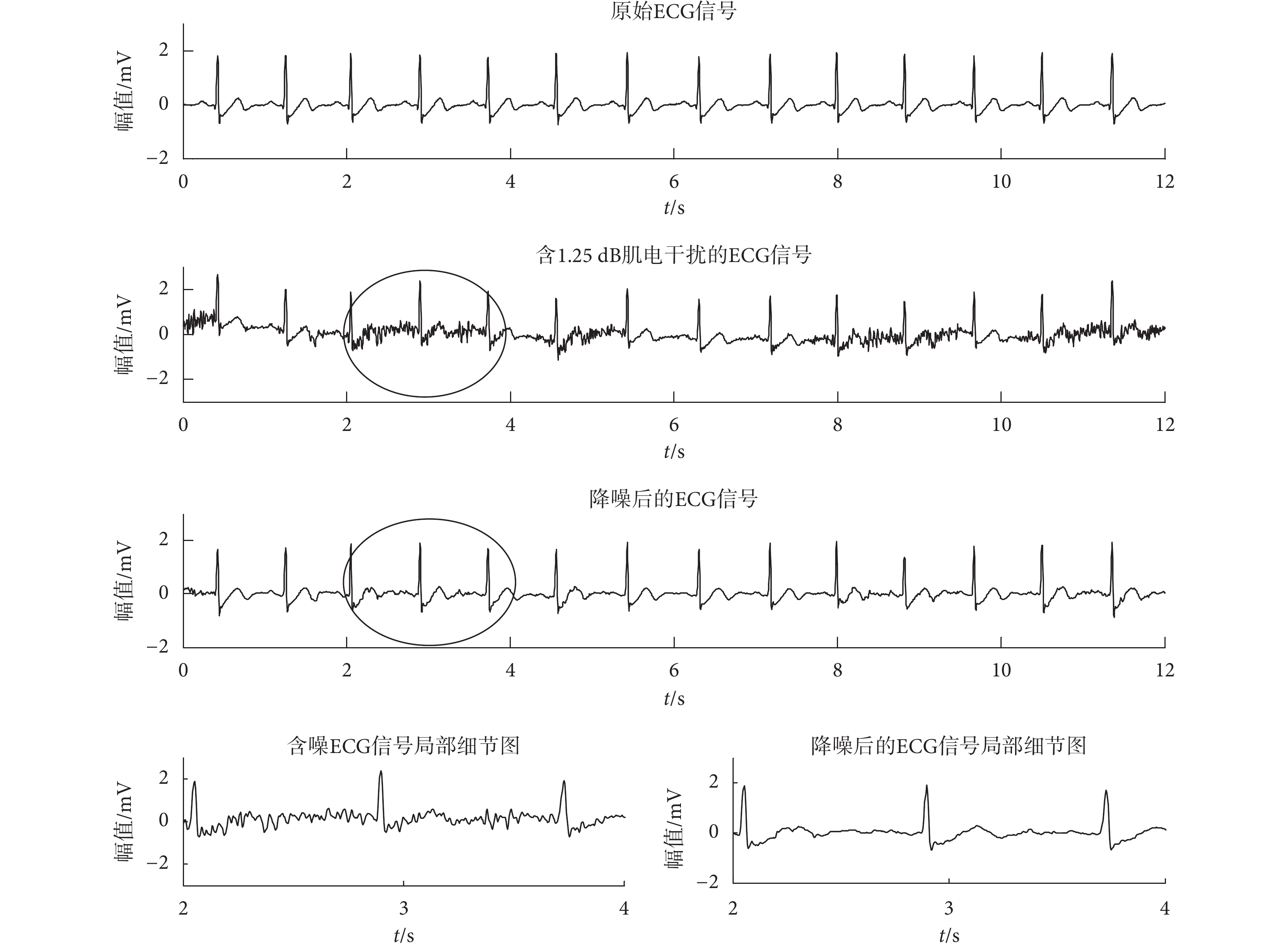圖4
濾除肌電干擾結果圖
Figure4.
Experimental results for muscle artifacts noise case
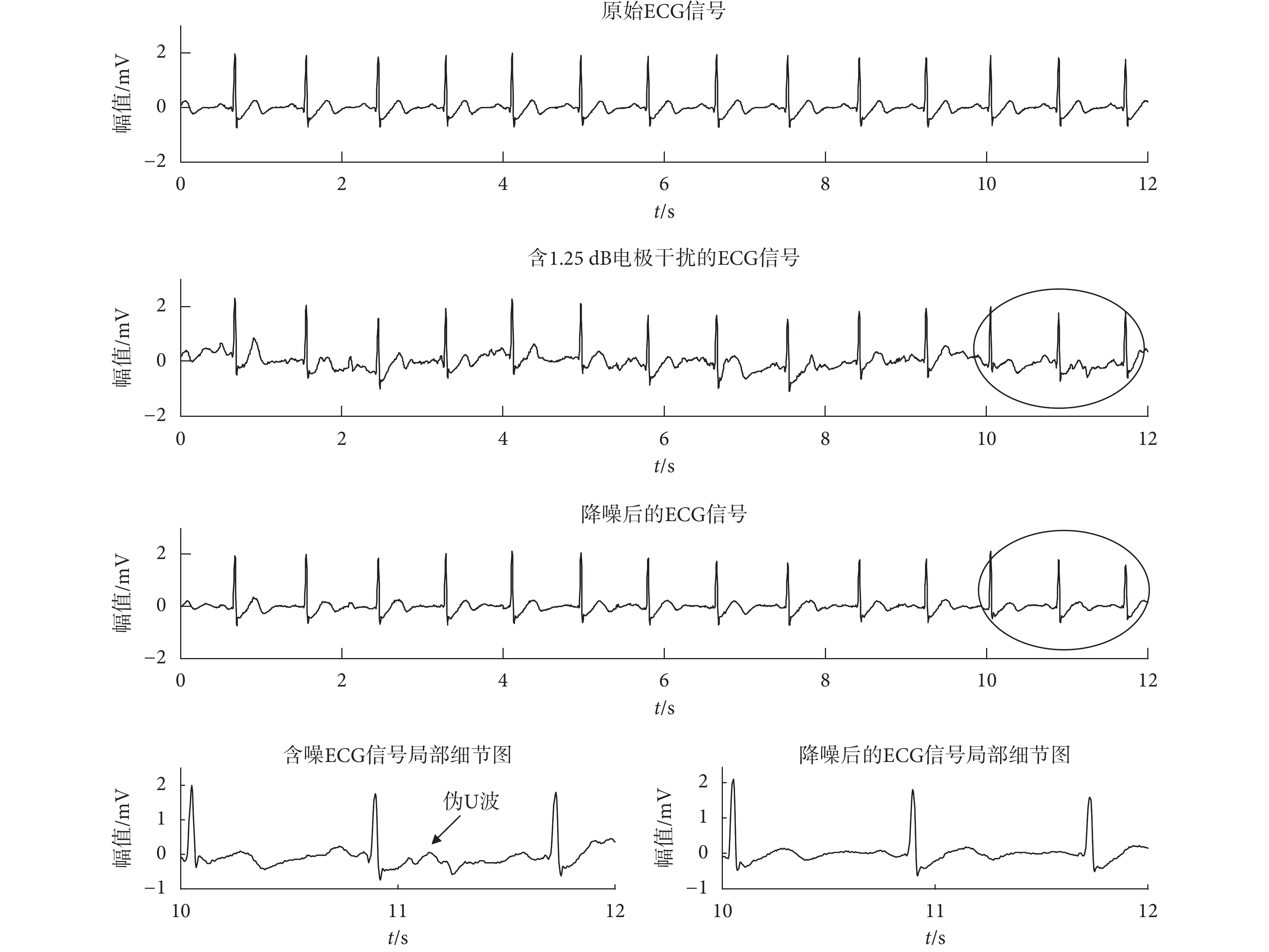
濾除 1.25 dB 電極干擾的實驗結果如圖 5 所示。其中，含噪 ECG 信號和原始 ECG 信號（以 103 號為例）相比較可以看出，電極干擾已經改變了原始 ECG 信號中特征波的形態，部分噪聲甚至在特征波未出現的地方模仿出了特征波的形態；并且由含噪 ECG 信號的局部細節圖可以發現，電極干擾不但更改了 P 波和 T 波的形態，更是模擬出了原本沒有的 U 波，使得正常的 T 波變成了 U 波增大型的 T 波。但經過本文提出的基于 RLS 在線訓練算法的 ESN 降噪算法降噪后的 ECG 信號和原始 ECG 信號相比較可以看出，本文的降噪算法很好地濾除了 ECG 信號中電極干擾，恢復了信號原有的形態特征，尤其從降噪后的 ECG 信號的局部細節圖可以發現，該降噪算法濾除了噪聲模擬出的偽 U 波，并對于 ECG 信號的 P 波和 T 波等微弱波形特征也有較高的復原度。
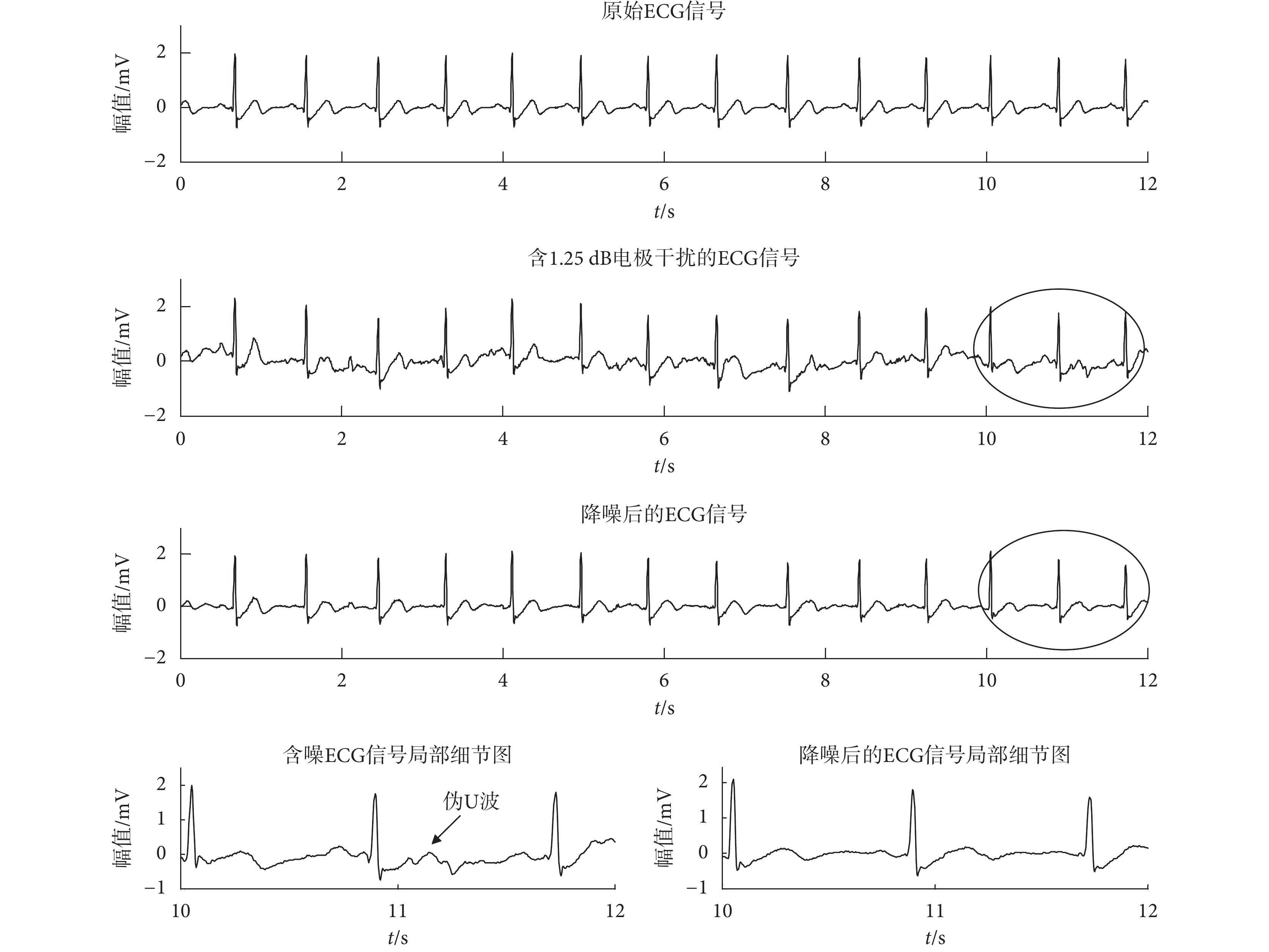圖5
濾除電極干擾結果圖
Figure5.
Experimental results for electrode motion noise case
如圖 3～圖 5 所示，3 種不同的噪聲（基線漂移、肌電干擾、電極干擾）都對 ECG 的形態產生了破壞，出現一些偽病態波形，比如基線改變、P 波消失或者偽 U 波出現等。而從每幅圖的原始信號和處理后的信號對比可以看出，本文提出的降噪算法很好地濾除了噪聲，并且由每幅圖降噪后的 ECG 信號局部細節圖可以發現，降噪后的 ECG 信號很好地恢復了原始信號的形態特征。對于一些微弱低頻成分，例如：P 波和 T 波，由于其幅值小頻率低，一方面導致其極易被噪聲淹沒或改變形態，另一方面也使得其在降噪過程中容易被當成噪聲濾除，但是在本文方法的降噪結果中，這些幅值很小的低頻細節特征也得到了很好的恢復和保持。
2.2.2 與其他降噪方法的比較
如表 1 所示，分別為 WT-Subband 法、S 變換法和本文所提出的基于 RLS 在線訓練算法的 ESN 降噪算法來濾除 0 dB、1.25 dB 及 5 dB 的基線漂移的實驗結果，選取 MIT-BIH 數據庫中共 9 個 ECG 數據的實驗結果，分別為：103 號、105 號、111 號、116 號、122 號、205 號、213 號、219 號、223 號。
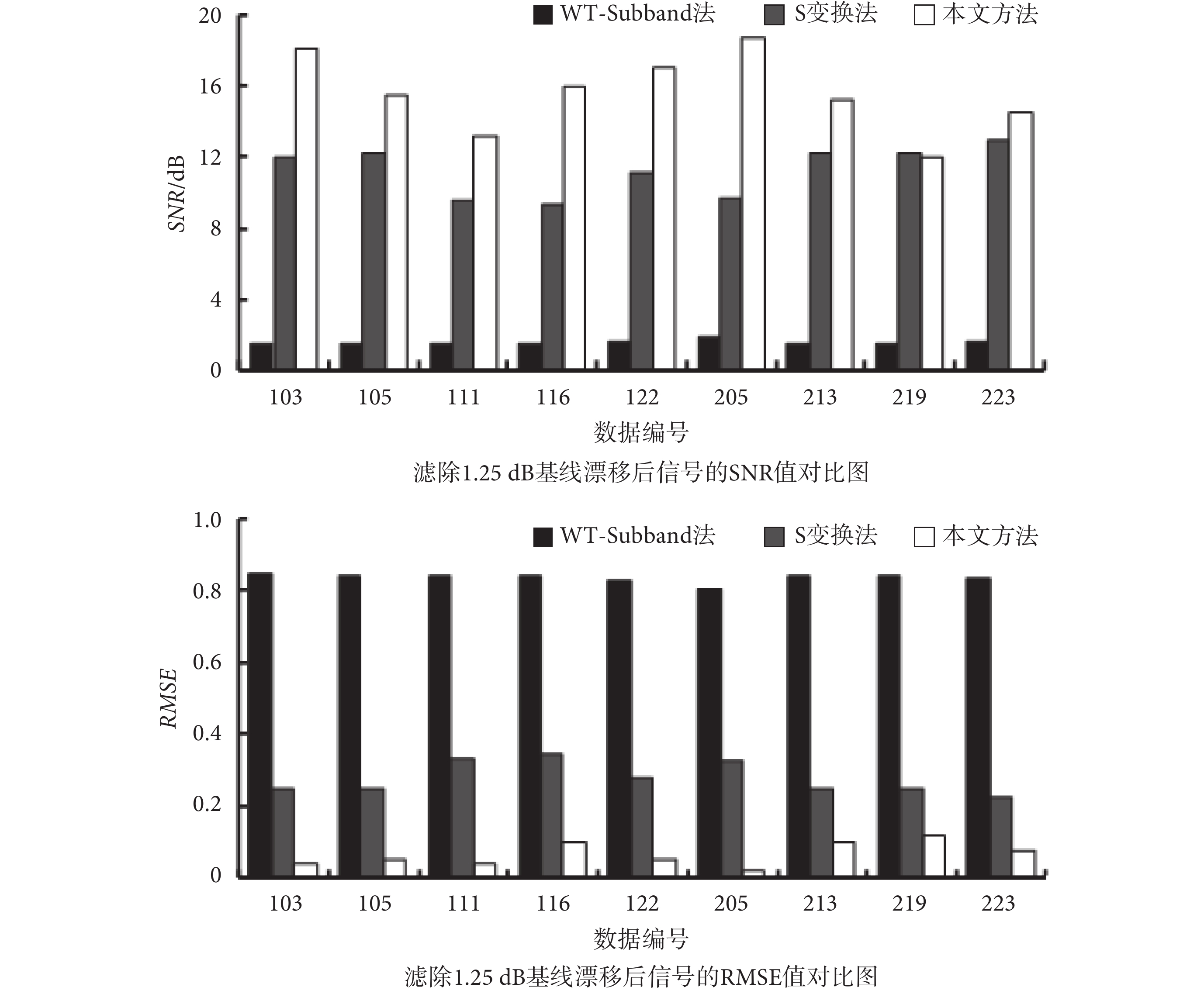
如圖 6 所示，以柱狀圖的形式展示了三種方法濾除 1.25 dB 噪聲后的結果。相比于使用前兩種方法降噪，使用本文提出的方法降噪后 SNR 和 RMSE 與前兩種方法相比有了明顯的改善，表明了本文所提出的算法可以有效地濾除基線漂移噪聲。例如，122 號數據疊加 1.25 dB 的基線漂移噪聲后，其經過 WT-Subband 法和 S 變換法降噪后的 SNR 值分別為 1.60 dB 和 11.17 dB，RMSE 值分別為 0.830 和 0.276；經本文提出的算法降噪后的 SNR 值達到了 17.13 dB，RMSE 值降為了 0.048。
其中 219 號數據的實驗結果中，本文所提出的方法與 S 變換法處理后的 SNR 值相差不多，RMSE 值則有相當大的提高，這是由于 219 號數據患者本身患有陣發性房顫，這導致其 ECG 信號中陣發性出現特異性心拍，且 RR 間期不正常。但其訓練集中出現特異性心拍的個數較少，測試集中較多。本文所提出的降噪算法是依據訓練集訓練后所保存的 ESN 網絡來進行降噪處理，當輸入與訓練樣本相差較大的數據時其實驗結果也會較差，同時如果其訓練樣本增多，其實驗結果也將更優。
表1
濾除基線漂移的實驗結果
Table1.
Experimental results for baseline wander noise
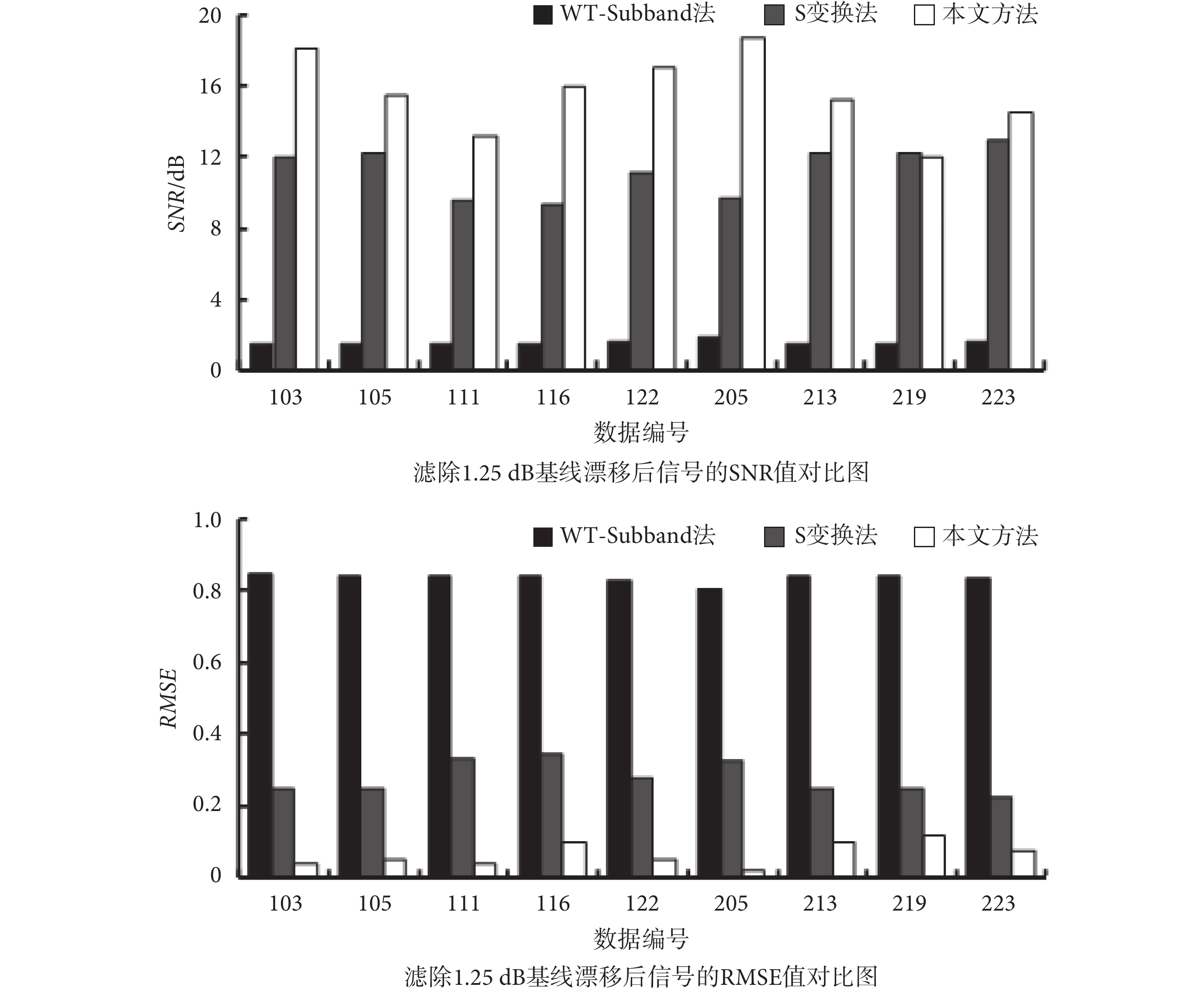圖6
濾除 1.25 dB 基線漂移的結果對比圖
Figure6.
De-noised results for 1.25 dB baseline wander noise case
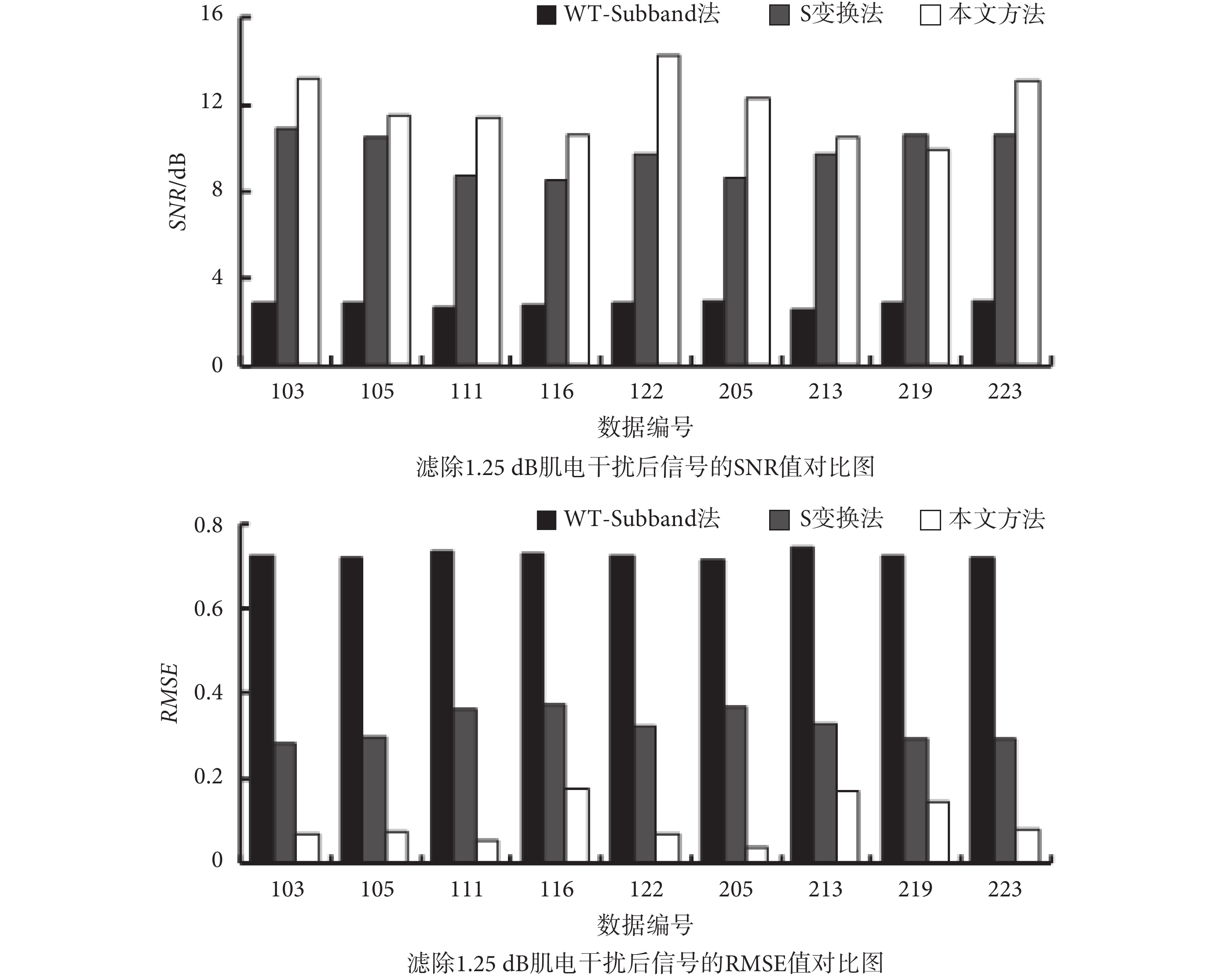
如表 2 所示，分別為采用 WT-Subband 法、S 變換法和本文所提出的基于 RLS 在線訓練算法的 ESN 降噪算法對含有肌電干擾的 ECG 信號進行濾波后的結果，并以柱狀圖的形式展示了這三種方法分別濾除 1.25 dB 噪聲后的 SNR 值和 RMSE 值，如圖 7 所示。相比于使用前兩種方法降噪，使用本文提出的方法降噪后 SNR 值和 RMSE 值與前兩種方法相比有了一定的改善，表明了本文提出的降噪算法可以有效地濾除肌電干擾。例如，122 號數據疊加 1.25 dB 的肌電干擾后，其經過 WT-Subband 法和 S 變換法降噪后的 SNR 值分別為 2.86 dB 和 9.67 dB，RMSE 值分別為 0.729 和 0.328；經本文提出的算法降噪后的 SNR 值達到了 14.27 dB，RMSE 值降為了 0.069。
表2
濾除肌電干擾的實驗結果
Table2.
Experimental results for muscle artifacts noise
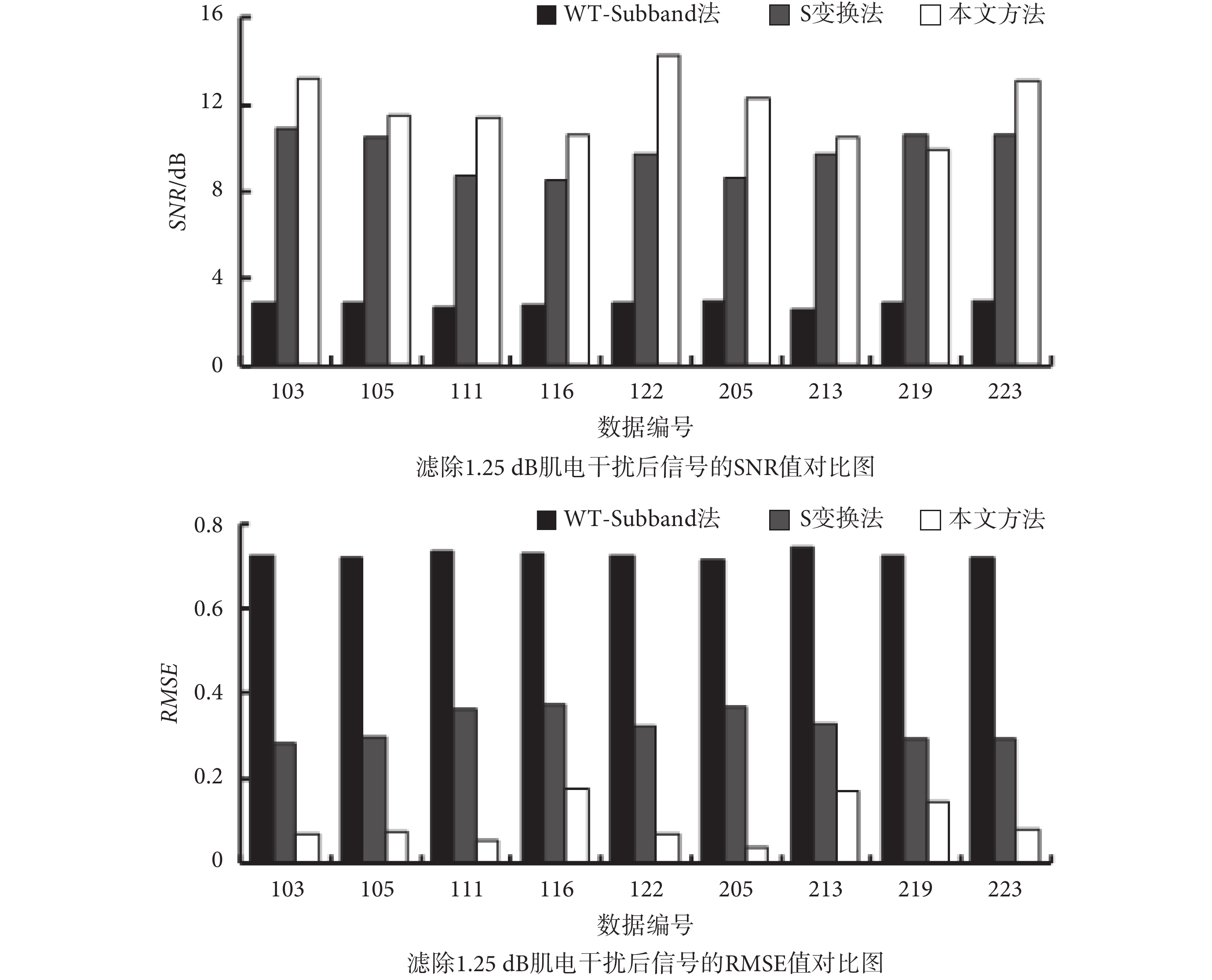圖7
濾除 1.25 dB 肌電干擾的結果對比圖
Figure7.
De-noised results for 1.25 dB muscle artifacts noise case
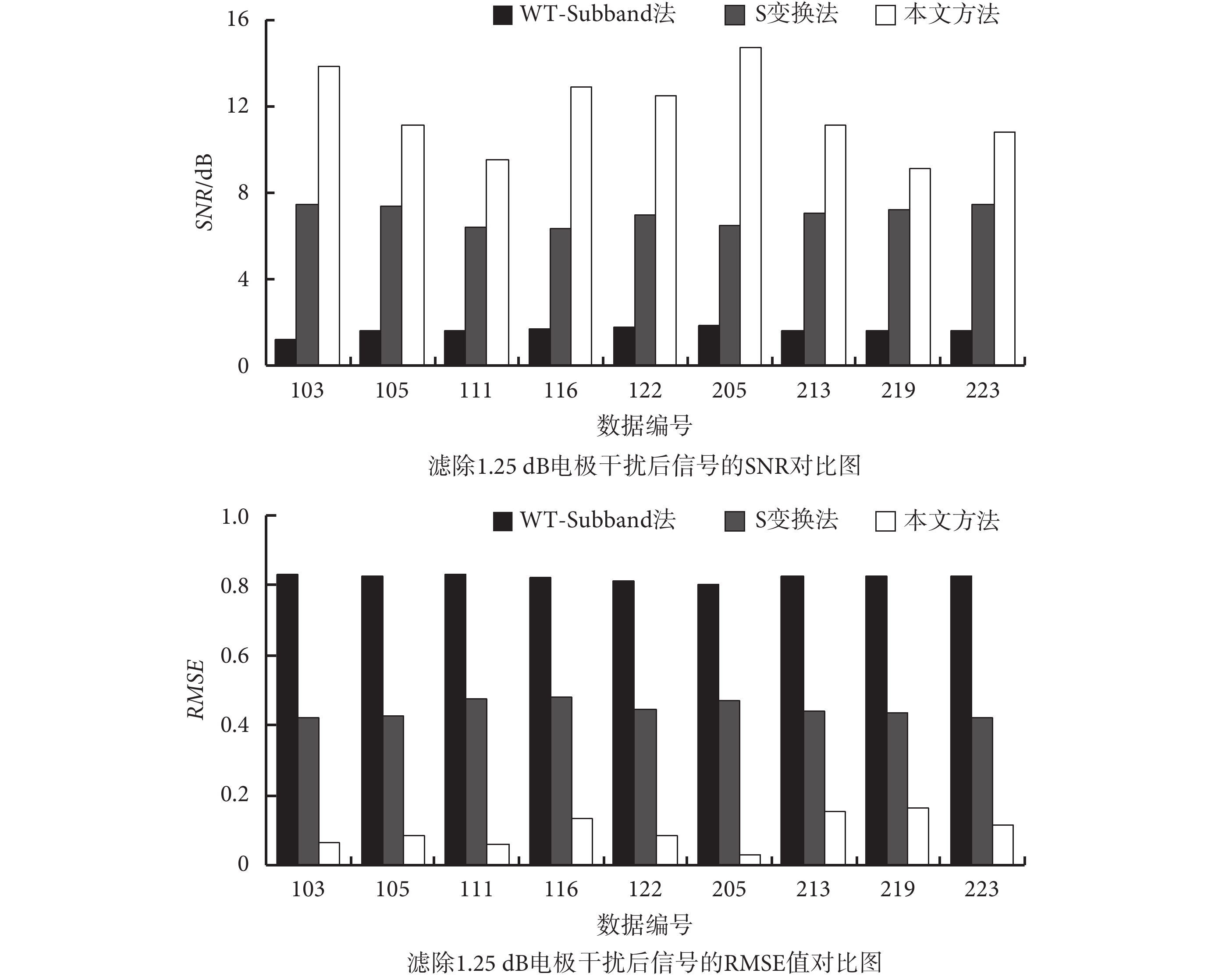
如表 3 所示，分別為采用 WT-Subband 法、S 變換法和本文所提出的基于 RLS 在線訓練算法的 ESN 降噪模型算法對含有電極干擾的 ECG 信號進行濾波后的實驗結果，如圖 8 所示，為三種方法分別濾除 1.25 dB 電極干擾后的 SNR 值和 RMSE 值。相比于使用前兩種方法降噪，使用本文提出的方法降噪后 SNR 值和 RMSE 值與前兩種方法相比有了很大的改善。例如，122 號數據疊加 1.25 dB 的電極干擾后，其經過 WT-Subband 法和 S 變換法降噪后的 SNR 值分別為 1.75 dB 和 6.96 dB，RMSE 值分別為 0.816 和 0.449；經本文提出的算法降噪后的 SNR 值達到了 12.48 dB，RMSE 值降為了 0.083。
表3
濾除電極干擾的實驗結果
Table3.
Experimental results for electrode motion noise
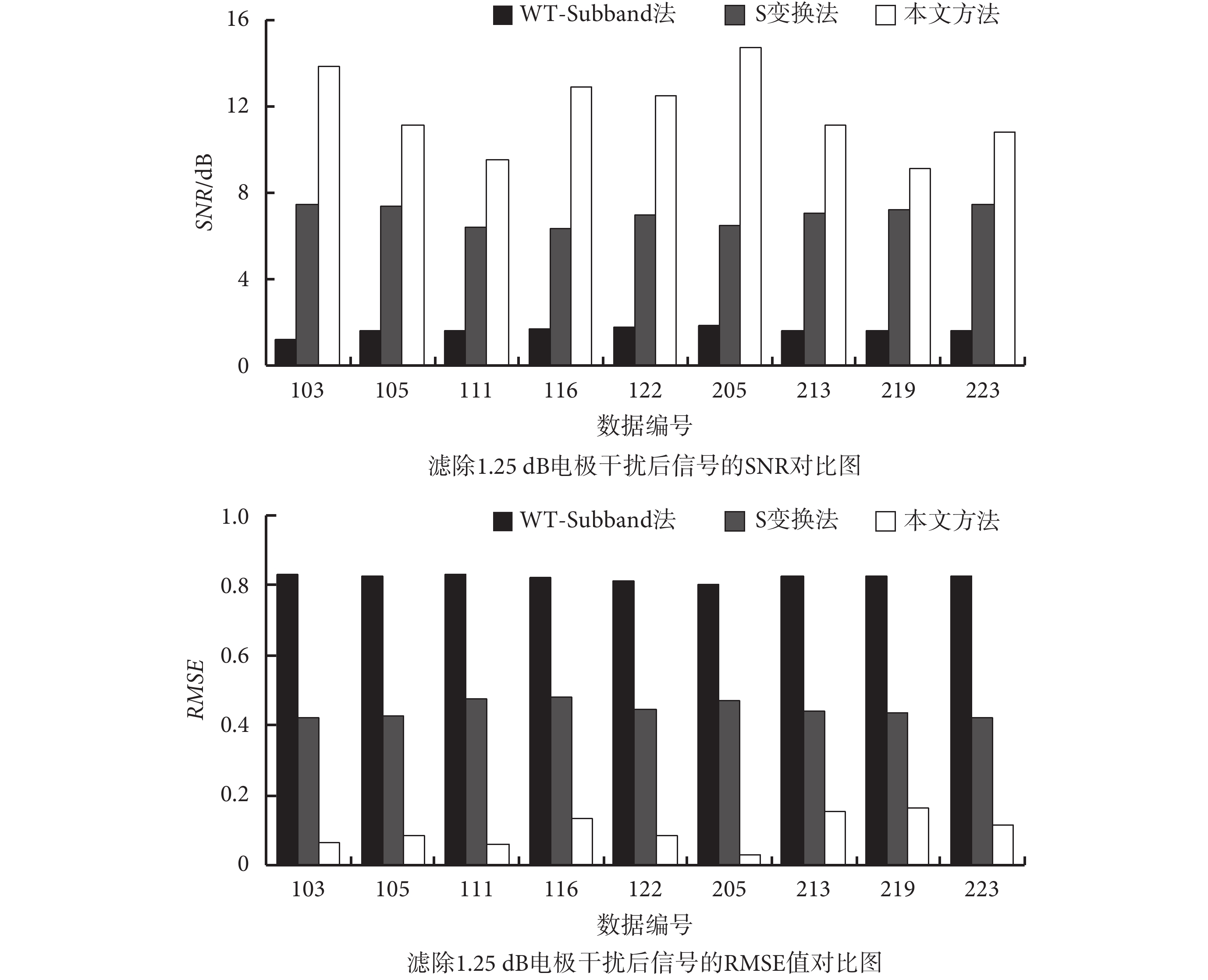圖8
濾除 1.25 dB 電極干擾的結果對比圖
Figure8.
De-noised results for 1.25 dB electrode motion noise case
從表 1～表 3 的這 3 個表中以及圖 6～圖 8 的三個柱狀圖中可以看出，與 WT-Subband 法和 S 變換法相比，本文基于 RLS 在線訓練算法的 ESN 降噪模型在去除 ECG 信號中的大噪聲時，無論是反映降噪效果總體誤差的 RMSE 值的降低，還是反映降噪后信號和噪聲的比值關系的 SNR 值的較大提高，都驗證了本文提出的基于 RLS 在線訓練算法的 ESN 降噪模型對 ECG 信號中的三種復雜噪聲有著較好的降噪效果。
3 結論
針對消除 ECG 信號包含的復雜噪聲并完整保留 ECG 信號的形態這一難題，本文提出了基于 RLS 在線訓練算法的 ESN 降噪模型。與 WT-Subband 法和 S 變換法的實驗結果對比表明，基于 RLS 在線訓練算法的 ESN 降噪模型的實驗結果在 SNR 值和 RMSE 值上都具有明顯優勢，能夠達到較好的降噪效果。并且，采用 MIT-BIH 數據庫中的數據進行對比實驗結果表明，該降噪模型在處理被噪聲污染較嚴重的 ECG 信號時，不僅有較好的降噪效果，而且 ECG 信號的低頻特征波也得到了很好的恢復和保持。綜上所述，本文實驗結果表明，本文所提出的降噪模型在心血管疾病的智能診斷的預處理階段具有很好的應用價值和實際意義。
引言
目前，由心血管病引起的死亡已占城鄉居民死亡構成的首位，并且心血管病患病率及死亡率仍處于上升階段[1]。動態心電圖（electrocardiogram，ECG）作為應用范圍最廣的診斷心血管疾病的重要無創性手段，其信號的低頻成分的變化對心血管疾病的智能診斷至關重要，例如 ST 段的變化是利用動態 ECG 信號診斷心肌梗死的重要指標之一[2]。如今，遠程醫療的發展為動態 ECG 信號的長期監測提供了平臺。但與此同時，遠程醫療背景下的信號采集和傳輸也混雜了多種因素造成的復雜噪聲，并且這些復雜噪聲也極易淹沒 ECG 信號的主要特征，特別是例如 P波、T 波等低頻成分。因此，如何消除 ECG 信號中的復雜噪聲，并完整保留 ECG 信號的主要特征，成為當前醫學信息處理領域亟待解決的難題。
目前，用于 ECG 信號降噪的方法主要有：人工神經網絡（artificial neural networks，ANN）、集合經驗模式分解（ensemble empirical mode decomposition，EEMD）、主成分分析（principal component analysis，PCA）、獨立成分分析（independent component analysis，ICA）、傅里葉變換、S 變換和小波變換等[3-11]。Jebaraj 等[4]利用 EEMD 將含噪 ECG 信號分解為若干個不同時間尺度的固有模態函數（intrinsic mode function，IMF），然后將這些 IMF 中含有噪聲的舍棄，最終能夠濾除含噪信號中 60 Hz 的電力線干擾。但是，在舍棄的 IMF 中也會含有與低頻噪聲的頻率相似的 ECG 的 P 波和 T 波，這就導致重構的 ECG 信號不完整。而 PCA 和 ICA 都是用于從非高斯噪聲信號中尋找獨立的源信號的盲源分離技術，能夠濾除與 ECG 信號統計不相關的噪聲[5-6]。但是，該類方法的魯棒性低，對于含噪 ECG 信號的細微變化十分敏感，并不適用于遠程醫療背景下 ECG 信號中含有復雜噪聲的情況。Alyasseri 等[11]首先利用 β 爬山算法選擇的最優的小波基將含噪 ECG 信號由時域變換到頻域的不同尺度中，再利用閾值保留主要由有效信號控制的小波系數，最終該方法在去除高頻大噪聲方面取得了不錯的結果。但對于 ECG 信號和噪聲的頻帶相互重疊的情況，主要保留的小波系數仍然含有部分噪聲信息，這也就必然導致重構的 ECG 信號的低頻成分存在形態失真。基于以上分析，現有研究成果在降噪精度上均得到了較滿意的效果，但并沒有過多地關注于 ECG 信號的低頻成分保持問題。
因此，為了進一步提高在遠程醫療背景下被復雜噪聲污染的 ECG 信號的降噪效果，尤其是對 ECG 信號低頻成分的保持，本文提出了基于遞歸最小二乘（recursive least square，RLS）的回聲狀態網絡（echo state network，ESN）算法——RLS-ESN 算法。該方法利用 RLS 來訓練 ESN，從而使網絡自動學習采集到的含噪 ECG 數據中非線性的且具有區分度的深層次特征，最后網絡利用這些能夠區分 ECG 信號和噪聲的特征自動重構得到干凈的 ECG 信號。
1 方法
如圖 1 所示，基于 RLS 在線訓練算法的 ESN 降噪框圖主要由 4 部分組成：預處理信號、初始化 ESN、構建輸入輸出函數和基于 RLS 的在線訓練網絡。首先，由于過大的采樣頻率會造成 ECG 信號中冗余信息增多降低網絡運行效率，而過小的采樣頻率又會丟失 ECG 信號中有效信息，因此本文算法對 ECG 信號以合適的 250 Hz 的采樣頻率進行重采樣；其次，依據網絡參數的范圍設置合適的 ESN 網絡參數；然后，為了更符合現實需求和 ECG 信號非平穩信號的特點，采用了逐個處理信號的 RLS 在線訓練算法對 ESN 進行訓練，利用儲備池的稀疏性能得到含噪 ECG 數據中非線性的且具有區分度的深層次特征，并且通過訓練得到最優的輸出權值矩陣，保存訓練好的 ESN 網絡；最后，將測試集中含噪 ECG 信號輸入訓練好的 ESN 網絡，利用儲備池得到能夠區分 ECG 信號和噪聲的特征后，訓練好的 ESN 網絡再利用輸出權值矩陣重構得到干凈的 ECG 信號。
圖1
基于 RLS 在線訓練算法的 ESN 降噪框圖
Figure1.
ECG signal filter block diagram of ESN with RLS online training algorithm
1.1 數據來源
本文實驗中使用的 ECG 信號來自美國麻省理工學院與貝斯以色列醫院（Massachusetts Institute of Technology and Beth Israel Hospital，MIT-BIH）聯合構建的數據庫中的心律失常數據庫（Arrhythmia Database）（網址為：https://www.physionet.org/physiobank/database/mitdb/），該數據庫中包括 48 組采樣頻率為 360 Hz 并且數據長度為 30 min 的動態 ECG 信號記錄，每組記錄包括來自醫用的 24 h 動態 ECG 信號記錄儀的 12 導聯數據中的兩個導聯信號：第一個導聯信號為修正的肢體Ⅱ導聯，第二個導聯信號為胸部 V2 導聯或胸部 V5 導聯[12]。為了與已有文獻中的采用基于子帶自適應閾值的小波變換（wavelet transform with subband dependent threshold，WT-Subband）降噪算法和 S 變換降噪算法進行比較，本文對應展示了 9 個 ECG 數據的實驗結果，分別為：103 號、105 號、111 號、116 號、122 號、205 號、213 號、219 號、223 號。
實驗中采用的噪聲信號來自于 MIT-BIH 數據庫中的噪聲壓力數據庫（Noise Stress Test Database）（網址為：https://www.physionet.org/physiobank/database/nstdb/），其中包括 3 h 的動態 ECG 信號記錄噪聲數據，分別為基線漂移（baseline wander，BW）、肌電干擾（muscle artifacts，MA）和電極干擾（electrode motion，EM）共 3 種噪聲數據。
1.2 基于 RLS-ESN 的 ECG 信號降噪算法
ESN 作為深度學習的主流模型之一，不但具有基于醫療大數據背景下數據增多效果更優的特點，而且還具有求解過程簡單且訓練速度快的特點。它的獨特之處在于其是采用由隨機稀疏連接的神經元組成的儲備池來代替傳統神經網絡中的隱藏層，并且唯一需要訓練的參數只有輸出權值矩陣，因此大大簡化了網絡權值的求解過程和訓練算法[13-14]。基于 ESN 的降噪算法是通過訓練網絡參數自動學習得到含噪 ECG 數據中非線性的且具有區分度的深層次特征，并利用這些特征以實現將 ECG 信號與噪聲分離的目的。
本文提出了基于 RLS 的在線訓練算法完成 ESN 降噪模型的權重更新。相比于離線訓練算法一次性的處理所有的輸入信號，以序列化的方式逐個處理輸入信號的基于 RLS 的在線算法更適合于目前信息處理的需求[15]。并且 RLS 的基本思想是在每個時刻對所有已輸入信號而言重估的平方誤差的加權和最小，這使得其對 ECG 信號這種非平穩信號的適應性非常好[16]。基于 RLS 在線訓練算法的 ESN 降噪模型的結構圖如圖 2 所示。
圖2
基于 RLS 在線訓練算法的 ESN 結構圖
Figure2.
The structure of ESN based on RLS online training algorithm
1.2.1 信號預處理
作為一種準周期性信號，ECG 信號有效信息主要分布在 P-QRS-T 波群中，冗余信息主要體現在相鄰樣本點之間的相關性和相鄰心拍之間的相似性[17]。因此，在處理同等時間長度的 ECG 信號時，過大的采樣頻率會導致數據冗余增多，并且冗余信息的增多不僅沒有為 ESN 降噪模型增添新的特征，反而會增大儲備池維度，降低 ESN 的計算速率增大計算誤差導致網絡運行性能降低；而過小的采樣頻率則直接會導致 ECG 信號中相關性等特征信息的丟失。
基于此，Petr?nas 等[18]根據人的心理電活動周期并且經過多次試驗得出，當 ECG 信號的頻率為 250 Hz 時，可以在包含 ECG 信號主要特征的前提下使用較低緯度的儲備池，以保證 ESN 的高效運行。因此本文預處理時，首先將 MIT-BIH 庫中的 48 組 ECG 數據以及 3 種噪聲數據重采樣為 250 Hz。然后，將 3 種噪聲數據按照一定的信噪比（signal-to-noise ratio，SNR）（以符號 SNR 表示）疊加到心律失常數據庫中的 48 組 ECG 信號上，即可得到含噪 ECG 信號。最后，利用每個原始 ECG 數據的前 3 min 信號和相應的含噪 ECG 數據的前 3 min 信號組成訓練集，剩余的含噪 ECG 信號組成測試集。
1.2.2 ESN 降噪模型的初始化
為消除 ECG 信號中的噪聲，需構建基于 RLS 在線訓練算法的 ESN 降噪模型。首先，進行參數的初始化。ESN 的主要參數包括：儲備池規模、儲備池稀疏程度、儲備池譜半徑和儲備池輸入單元尺度[19]。儲備池規模（符號記為：N）定義為儲備池中的神經元的個數，在儲備池內部通過這 N 個神經元之間稀疏連接形成 N × N 的儲備池內部神經元連接權值矩陣 W。儲備池稀疏程度（符號記為：SD）定義為儲備池中相互連接的神經元個數與總神經元個數之比，表達式為 SD = m/N，通常 SD 的取值為 1%～5%。儲備池譜半徑（符號記為：SR）定義為 W 的最大特征值的絕對值，表達式為 SR = max{abs（W 的特征值）}，且當 SR < 1 時，ESN 才具有回聲狀態性質。儲備池輸入單元尺度（符號記為： IS）是一個尺度因子，在輸入信號連接至儲備池之前與輸入信號相乘，將輸入信號變換至神經元激活函數相應的范圍內。
其次，進行權值矩陣的初始化。輸入單元與儲備池內部連接的的權值矩陣 Win 和儲備池內部神經元連接權值矩陣 W 的初始化都是隨機且服從均勻分布的，且初始給定后固定不變。而儲備池與輸出單元連接權值矩陣 Wout 和輸出單元與儲備池的連接權值矩陣 Wback 初始化為零矩陣，其中 Wout 通過訓練得到其最終值。
1.2.3 輸入輸出信號的構建
ESN 的輸入信號 xr（n）的表達式如式（1）所示。其中，x（n）為當前時刻的含噪 ECG 信號；x（n-1）為上一時刻的含噪 ECG 信號；x′（n）和 x″（n）分別為 x（n）的一階導和二階導，表征了 x（n）的細節特征。
|
'/> |
輸出信號 y（n）為濾波后的 ECG 信號，定義如式（2）所示：
|
其中， g（·）為激活函數，在實驗中選為恒等函數，即輸出神經元為一個線性神經元；矩陣 v（n）的表達式為
，其中 r（n）是儲備池的狀態矩陣。
誤差定義為當前時刻的干凈 ECG 信號 d（n）與 y（n）的差值，表達式為 e（n）= d（n）– y（n），其中 d（n）為當前時刻的干凈 ECG 信號。因此，在訓練中需要通過更新 Wout 和 r（n）使濾波后的 ECG 信號 y（n）逼近干凈 ECG 信號 d（n），使誤差 e（n）能夠近似于 0。
1.2.4 基于 RLS 的在線訓練
在本文中，輸出權重 Wout 的更新選用基于 RLS 的在線訓練算法[20]。具體過程如下：
（1）u（n）的表達式為
，其中 ψ（n）為 v（n）的相關系數矩陣的逆矩陣，并且 ψ（n）的更新如式（3）、式（4）所示：
|
|
式中的遺忘因子
定義為一個范圍為 0.95 <
< 1 的常數。設定
，其中 I 為單位矩陣，δ 為一個極小的正數。
（2）輸出權重的更新如式（5）所示：
|
（3）儲備池狀態矩陣 r（n）的更新，如式（6）所示：
|
其中 Win 為 4 × N 的輸入權值矩陣；W 為 N × N 的儲備池內部權值矩陣；f（·）為儲備池的激活函數，在實驗中選為非線性的 tanh（·）函數；遺忘率
被定義為一個小于 1 的正數。
2 結果與討論
2.1 性能指標
通過比較濾波后的信號與原始信號之間的 SNR 和均方根誤差（root mean square error，RMSE）（以符號 RMSE 表示）來評估本文降噪算法的性能。若 di 表示干凈 ECG 信號，yi 表示經過網絡降噪后的估計 ECG 信號，SNR 定義為信號和噪聲的比值，單位為分貝（dB），作為評價信號質量的重要指標，SNR 值越高說明濾波效果越好，表達式如式（7）所示：
|
RMSE 是一個無量綱參數，定義為估計信號和真實信號的差值，越低則說明濾波性能越好，表達式如式（8）所示：
|
2.2 實驗結果與討論
本文經過多次實驗后，網絡參數初始化為 SR = 0.4，SD = 2%，λ = 0.999 9，δ = 0.001 72，α = 0.8，IS = ［0.01；0.01；0.9；0.8］，輸入神經元個數為 4，儲備池規模 N 為 1 000，輸出神經元個數為 1。
2.2.1 實驗結果
濾除 1.25 dB 基線漂移的實驗結果如圖 3 所示。其中，含噪 ECG 信號和原始 ECG 信號（以 MIT-BIH 數據庫中 103 號為例）相比較可以看出，基線漂移的存在已經影響了整體波形的走勢；并且由含噪信號的局部細節圖可以看出，基線漂移使得正常的 ST 段抬高成為凸面向上型。但經過本文提出的基于 RLS 在線訓練算法的 ESN 降噪算法降噪后的 ECG 信號和原始 ECG 信號相比較可以看出，降噪后的信號回到了基線，且形態和原始信號基本保持一致，尤其從降噪后的 ECG 信號的局部細節圖可以發現，ECG 信號的 ST 段已恢復為正常的波形。
圖3
濾除基線漂移結果圖
Figure3.
Experimental results for baseline wander noise case
濾除 1.25 dB 肌電干擾的實驗結果如圖 4 所示。其中，含噪 ECG 信號和原始 ECG 信號（以 103 號為例）相比較可以看出，肌電干擾已嚴重破壞了 ECG 信號中特征波的形態；并且由含噪 ECG 信號的局部細節圖可以發現，Q 波和 S 波、P 波、T 波等低頻成分已經被肌電干擾完全淹沒，僅剩下了幅值較大的 R 波，造成了 ECG 信號的低頻特征丟失。但經過本文提出的基于 RLS 在線訓練算法的 ESN 降噪算法降噪后的 ECG 信號和原始 ECG 信號相比較可以看出，本文的降噪算法在濾除肌電干擾時，完整地保留了原有波形的形態特征，尤其從降噪后的 ECG 信號的局部細節圖可以發現，ECG 信號的低頻波形特征也得到了很好的保留。
圖4
濾除肌電干擾結果圖
Figure4.
Experimental results for muscle artifacts noise case
濾除 1.25 dB 電極干擾的實驗結果如圖 5 所示。其中，含噪 ECG 信號和原始 ECG 信號（以 103 號為例）相比較可以看出，電極干擾已經改變了原始 ECG 信號中特征波的形態，部分噪聲甚至在特征波未出現的地方模仿出了特征波的形態；并且由含噪 ECG 信號的局部細節圖可以發現，電極干擾不但更改了 P 波和 T 波的形態，更是模擬出了原本沒有的 U 波，使得正常的 T 波變成了 U 波增大型的 T 波。但經過本文提出的基于 RLS 在線訓練算法的 ESN 降噪算法降噪后的 ECG 信號和原始 ECG 信號相比較可以看出，本文的降噪算法很好地濾除了 ECG 信號中電極干擾，恢復了信號原有的形態特征，尤其從降噪后的 ECG 信號的局部細節圖可以發現，該降噪算法濾除了噪聲模擬出的偽 U 波，并對于 ECG 信號的 P 波和 T 波等微弱波形特征也有較高的復原度。
圖5
濾除電極干擾結果圖
Figure5.
Experimental results for electrode motion noise case
如圖 3～圖 5 所示，3 種不同的噪聲（基線漂移、肌電干擾、電極干擾）都對 ECG 的形態產生了破壞，出現一些偽病態波形，比如基線改變、P 波消失或者偽 U 波出現等。而從每幅圖的原始信號和處理后的信號對比可以看出，本文提出的降噪算法很好地濾除了噪聲，并且由每幅圖降噪后的 ECG 信號局部細節圖可以發現，降噪后的 ECG 信號很好地恢復了原始信號的形態特征。對于一些微弱低頻成分，例如：P 波和 T 波，由于其幅值小頻率低，一方面導致其極易被噪聲淹沒或改變形態，另一方面也使得其在降噪過程中容易被當成噪聲濾除，但是在本文方法的降噪結果中，這些幅值很小的低頻細節特征也得到了很好的恢復和保持。
2.2.2 與其他降噪方法的比較
如表 1 所示，分別為 WT-Subband 法、S 變換法和本文所提出的基于 RLS 在線訓練算法的 ESN 降噪算法來濾除 0 dB、1.25 dB 及 5 dB 的基線漂移的實驗結果，選取 MIT-BIH 數據庫中共 9 個 ECG 數據的實驗結果，分別為：103 號、105 號、111 號、116 號、122 號、205 號、213 號、219 號、223 號。
如圖 6 所示，以柱狀圖的形式展示了三種方法濾除 1.25 dB 噪聲后的結果。相比于使用前兩種方法降噪，使用本文提出的方法降噪后 SNR 和 RMSE 與前兩種方法相比有了明顯的改善，表明了本文所提出的算法可以有效地濾除基線漂移噪聲。例如，122 號數據疊加 1.25 dB 的基線漂移噪聲后，其經過 WT-Subband 法和 S 變換法降噪后的 SNR 值分別為 1.60 dB 和 11.17 dB，RMSE 值分別為 0.830 和 0.276；經本文提出的算法降噪后的 SNR 值達到了 17.13 dB，RMSE 值降為了 0.048。
其中 219 號數據的實驗結果中，本文所提出的方法與 S 變換法處理后的 SNR 值相差不多，RMSE 值則有相當大的提高，這是由于 219 號數據患者本身患有陣發性房顫，這導致其 ECG 信號中陣發性出現特異性心拍，且 RR 間期不正常。但其訓練集中出現特異性心拍的個數較少，測試集中較多。本文所提出的降噪算法是依據訓練集訓練后所保存的 ESN 網絡來進行降噪處理，當輸入與訓練樣本相差較大的數據時其實驗結果也會較差，同時如果其訓練樣本增多，其實驗結果也將更優。
表1
濾除基線漂移的實驗結果
Table1.
Experimental results for baseline wander noise
圖6
濾除 1.25 dB 基線漂移的結果對比圖
Figure6.
De-noised results for 1.25 dB baseline wander noise case
如表 2 所示，分別為采用 WT-Subband 法、S 變換法和本文所提出的基于 RLS 在線訓練算法的 ESN 降噪算法對含有肌電干擾的 ECG 信號進行濾波后的結果，并以柱狀圖的形式展示了這三種方法分別濾除 1.25 dB 噪聲后的 SNR 值和 RMSE 值，如圖 7 所示。相比于使用前兩種方法降噪，使用本文提出的方法降噪后 SNR 值和 RMSE 值與前兩種方法相比有了一定的改善，表明了本文提出的降噪算法可以有效地濾除肌電干擾。例如，122 號數據疊加 1.25 dB 的肌電干擾后，其經過 WT-Subband 法和 S 變換法降噪后的 SNR 值分別為 2.86 dB 和 9.67 dB，RMSE 值分別為 0.729 和 0.328；經本文提出的算法降噪后的 SNR 值達到了 14.27 dB，RMSE 值降為了 0.069。
表2
濾除肌電干擾的實驗結果
Table2.
Experimental results for muscle artifacts noise
圖7
濾除 1.25 dB 肌電干擾的結果對比圖
Figure7.
De-noised results for 1.25 dB muscle artifacts noise case
如表 3 所示，分別為采用 WT-Subband 法、S 變換法和本文所提出的基于 RLS 在線訓練算法的 ESN 降噪模型算法對含有電極干擾的 ECG 信號進行濾波后的實驗結果，如圖 8 所示，為三種方法分別濾除 1.25 dB 電極干擾后的 SNR 值和 RMSE 值。相比于使用前兩種方法降噪，使用本文提出的方法降噪后 SNR 值和 RMSE 值與前兩種方法相比有了很大的改善。例如，122 號數據疊加 1.25 dB 的電極干擾后，其經過 WT-Subband 法和 S 變換法降噪后的 SNR 值分別為 1.75 dB 和 6.96 dB，RMSE 值分別為 0.816 和 0.449；經本文提出的算法降噪后的 SNR 值達到了 12.48 dB，RMSE 值降為了 0.083。
表3
濾除電極干擾的實驗結果
Table3.
Experimental results for electrode motion noise
圖8
濾除 1.25 dB 電極干擾的結果對比圖
Figure8.
De-noised results for 1.25 dB electrode motion noise case
從表 1～表 3 的這 3 個表中以及圖 6～圖 8 的三個柱狀圖中可以看出，與 WT-Subband 法和 S 變換法相比，本文基于 RLS 在線訓練算法的 ESN 降噪模型在去除 ECG 信號中的大噪聲時，無論是反映降噪效果總體誤差的 RMSE 值的降低，還是反映降噪后信號和噪聲的比值關系的 SNR 值的較大提高，都驗證了本文提出的基于 RLS 在線訓練算法的 ESN 降噪模型對 ECG 信號中的三種復雜噪聲有著較好的降噪效果。
3 結論
針對消除 ECG 信號包含的復雜噪聲并完整保留 ECG 信號的形態這一難題，本文提出了基于 RLS 在線訓練算法的 ESN 降噪模型。與 WT-Subband 法和 S 變換法的實驗結果對比表明，基于 RLS 在線訓練算法的 ESN 降噪模型的實驗結果在 SNR 值和 RMSE 值上都具有明顯優勢，能夠達到較好的降噪效果。并且，采用 MIT-BIH 數據庫中的數據進行對比實驗結果表明，該降噪模型在處理被噪聲污染較嚴重的 ECG 信號時，不僅有較好的降噪效果，而且 ECG 信號的低頻特征波也得到了很好的恢復和保持。綜上所述，本文實驗結果表明，本文所提出的降噪模型在心血管疾病的智能診斷的預處理階段具有很好的應用價值和實際意義。
